[MIT]파이썬을 이용한 알고리즘의 이해 5. 일정 탐색과 이진 탐색 트리.
www.edwith.org/introalgorithm/lecture/26423/
[LECTURE] 일정 예약과 이진 탐색 트리 : edwith
강의 내용 - 활주로 예약 시스템의 정리 - 활주로 예약 시스템: 리스트로 해결하는 방법 - 이진 탐색 트리 : 계산 과정 학습 하기 - 커넥트재단
www.edwith.org
2011년 가을에 진행된 강의다.
컴퓨터 없이 칠판에 파이썬 문법을 활용한 알고리즘을 설명한다.
엘리스코딩에서 아이패드로 필기하는 형식의 강의를 들을 때 저런 개발새발 글씨로 필기를 왜 하며 그걸 왜 보여주고 말하는 식으로 강의를 하나, 굉장히 비효율적이라고 생각했는데
이러한 형식의 칠판 필기 강의를 오래간만에 보다 보니 (필자의 모교는 화이트보드 혹은 PPT를 활용한 강의를 했다...)
빠르게 진행되었으면 놓치기 쉬울 내용도 천천한 호흡으로 따라가기 좋다는, 그리고 그만큼 생각할 시간을 벌 수 있다는 장점을 깨달았다.
때로는 천천히 진행되는 강의가 좋을 때도 있다.

네이버 AI 부스트캠프에서 필요한 사전 지식에 '이진탐색트리'가 있어 네이버 edwith에 검색해 본 결과 이 강의를 찾을 수 있었다. 5강인 이 강의만 들어본 후기로는 매우 만족스럽고, 다음 강의는 물론이고 이전 강의들까지 다 듣고 싶다.
그리고 교수님 꽤 수업 잘 한다.
문제 :


비행기의 착률 요청 순서를 예약하고 싶다.
각각의 비행기 착륙 시간은 t이다.
R : 착륙 시간의 집합이다. (시간 t로부터 k분 안에 다른 착륙 스케줄이 없다면.)
k는 매개변수. 3분-4분 등으로 정할 수 있음. 기상 조건 등에 의해서 더 큰 폭으로 변할 수 있음.
오늘은 k= 3분으로 한다.
비행기가 착륙할 때마다 특정 시간을 R집합에서 제거해야 한다.
비행기가 착륙을 하고 나면 비행기가 착륙했던 특정한 t값 제공한다.
얼마나 자주 확인하든 정확한 값을 자료구조에서 제거하는 게 중요하다.
전 과정을 O(log n)이라는 시간 안에 끝내고 싶다. n은 집합의 크기다. (로그를 선형으로 바꿀 생각은 하지 않는 게 좋다.)
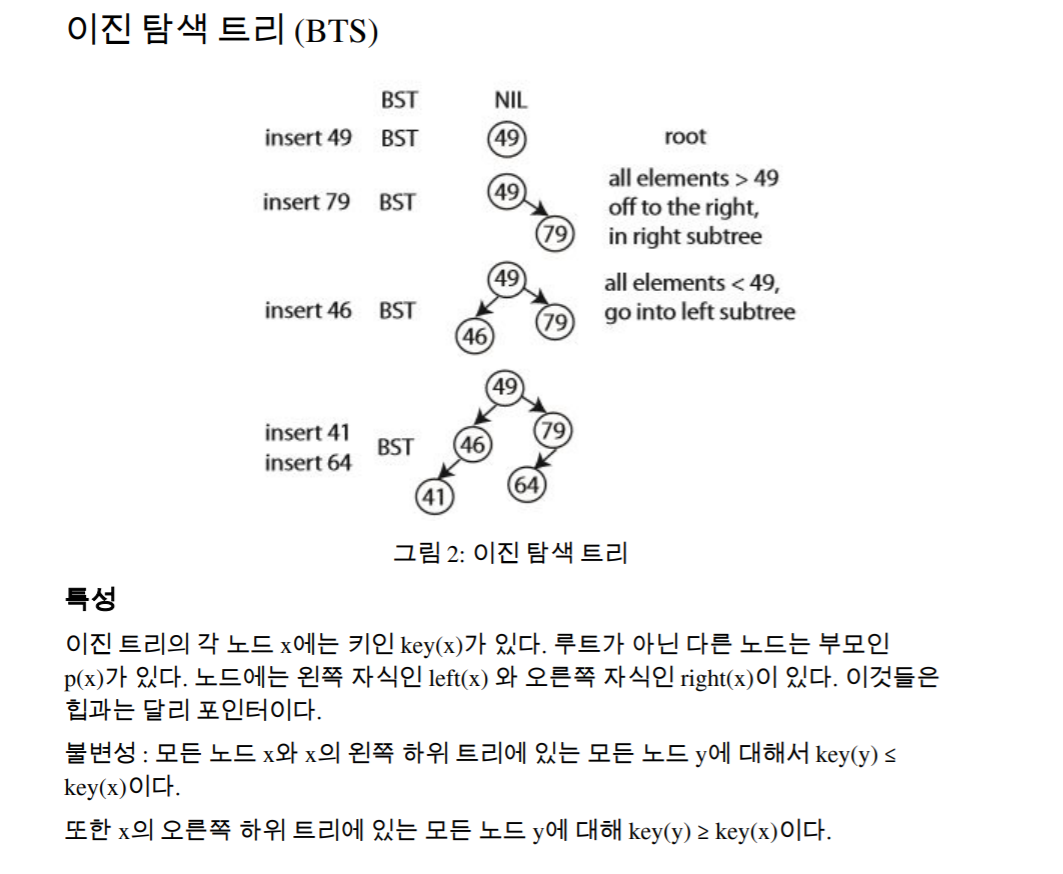
이진 탐색 트리의 장점은 힙보다 더 좋은 불변성을 제공한다는 것이다.
이진 탐색 트리는 포인터를 가진 트리로, 위로든 아래로든 갈 수 있다.
다시 문제로 돌아가서
적절한 삽입 지점을 찾는 동안 추가적인 확인이 가능하다. (k시간 확인처럼.)
최소값은 트리의 왼쪽을 따라가면 된다. 최대값은? 오른쪽을 따라가면 된다.
복잡도는 트리의 높이이다. O(h).
추가 문제
Rank(t) : 몇 대의 비행기가 t이하의 시각에 착륙 예정인가?
t분 전에 어떤 비행기가 착륙하나?
[MIT]파이썬을 이용한 알고리즘의 이해
'개발' 카테고리의 다른 글
| 코랩 Colab 폰트 맞춤설정하는 방법 (0) | 2021.02.11 |
|---|---|
| 리디셀렉트 - 데이터 분석가의 숫자유감 (1) | 2021.01.24 |
| Cousera 선결제취소 후 수료증 취득 (1) | 2020.11.22 |
| 코드스테이츠 AI 부트캠프 파이썬 사전과제 (3) | 2020.11.18 |
| 이상하고 어색한 문장 검색기 만들기#3 (0) | 2020.09.17 |


